Discrete Geodesic Parallel Coordinates

Publication

ACM Transactions on Graphics

Authors

Hui Wang, Davide Pellis, Florian Rist, Helmut Pottmann, Christian Müller

PDF

paper

Abstract

Geodesic parallel coordinates are orthogonal nets on surfaces where one of the two families of parameter lines are geodesic curves. We describe a discrete version of these special surface parameterizations and show that they are very useful for specific applications, most of which are related to the design and fabrication of surfaces in architecture. With the new discrete surface model, it is easy to control strip widths between neighboring geodesics. This facilitates tasks such as cladding a surface with strips of originally straight flat material or designing geodesic gridshells and timber rib shells. It is also possible to model nearly developable surfaces. These are characterized by geodesic strips with almost constant strip widths and are used for generating shapes that can be manufactured from materials which allow for some stretching or shrinking like felt, leather, or thin wooden boards. Most importantly, we show how to constrain the strip width parameters to model a class of intrinsically symmetric surfaces. These surfaces are isometric to surfaces of revolution and can be covered with doubly-curved panels that are produced with only a few molds when working with flexible materials like metal sheets.

Figures

Fig.: Architectural design in reference to designs by architect Frank Gehry. In our case the four surface patches are not developable, but are isometric to the same surface of revolution. The rectangular metal sheets covering the surface can be produced using just one comparably small sector between two meridian curves of the corresponding surface of revolution as a mold (left and Figure 16). The long vertical strip (left; gray) of the surface of revolution is either one big mold or can be segmented into smaller molds if necessary. Metal sheets covering surface areas with almost vanishing Gaussian curvature can be produced without a special mold, i.e., as developable surface patches.

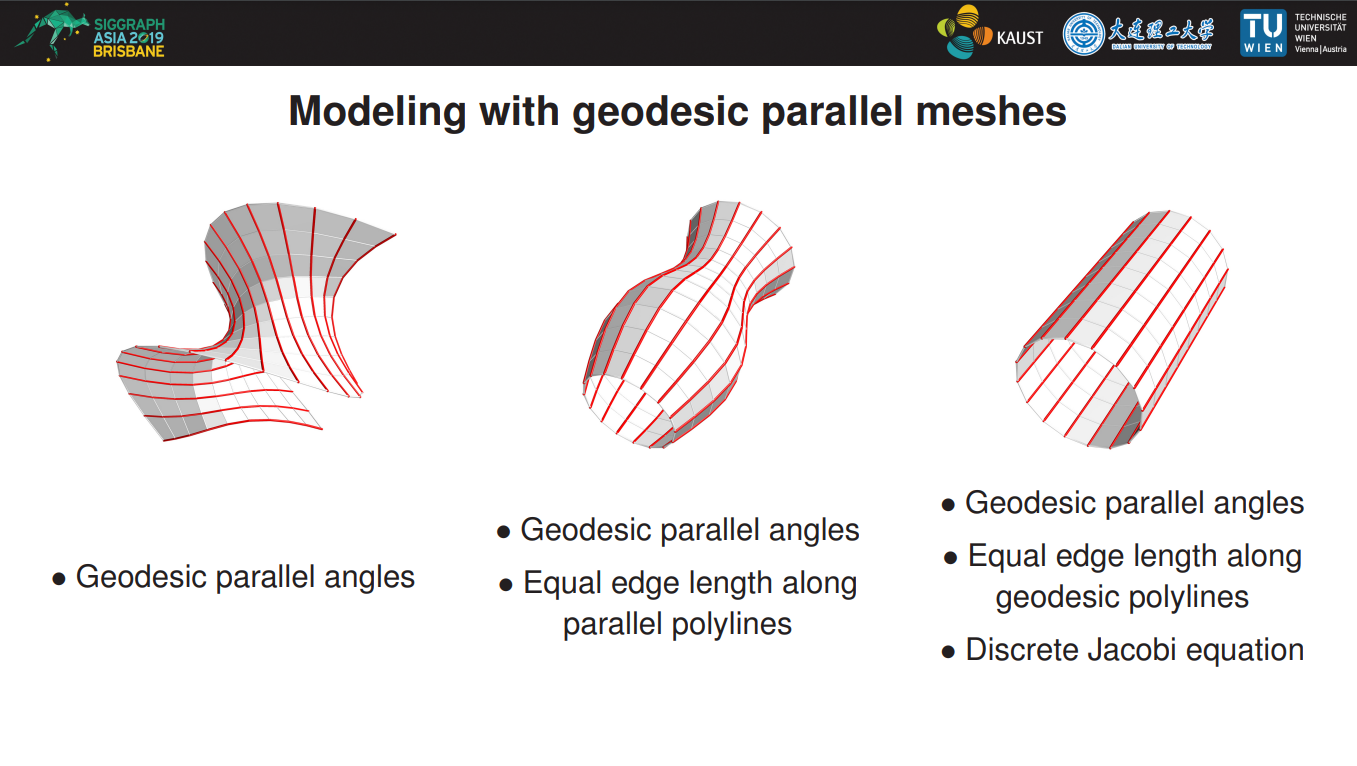
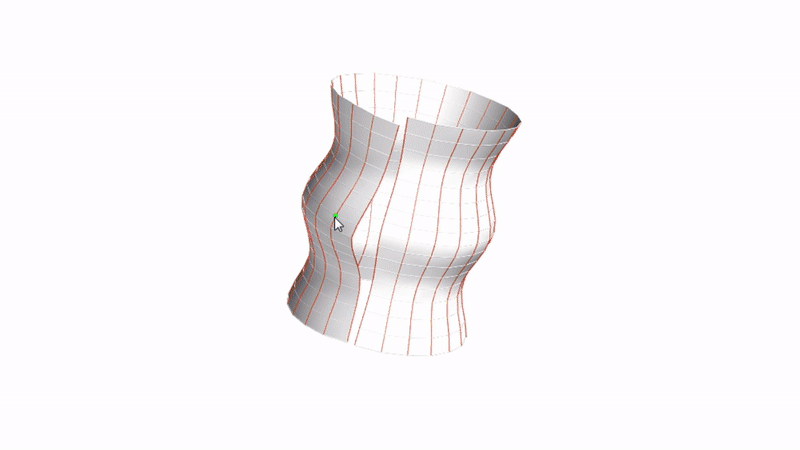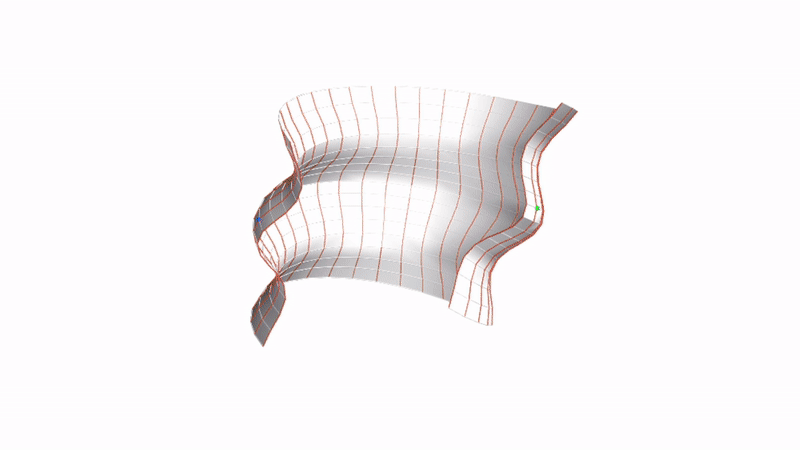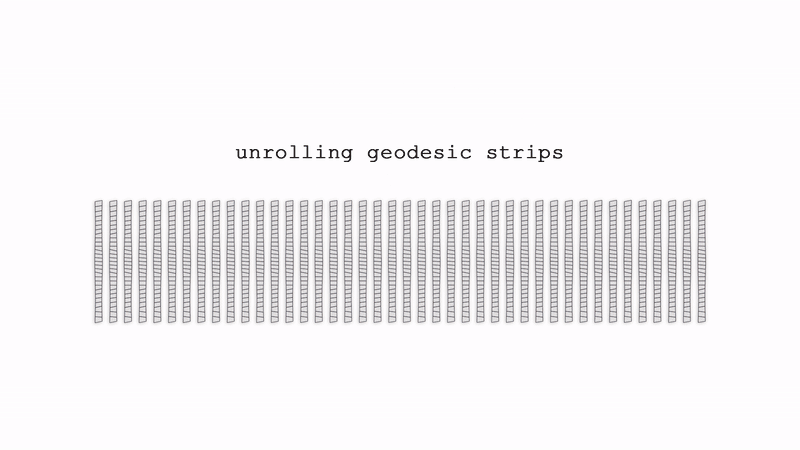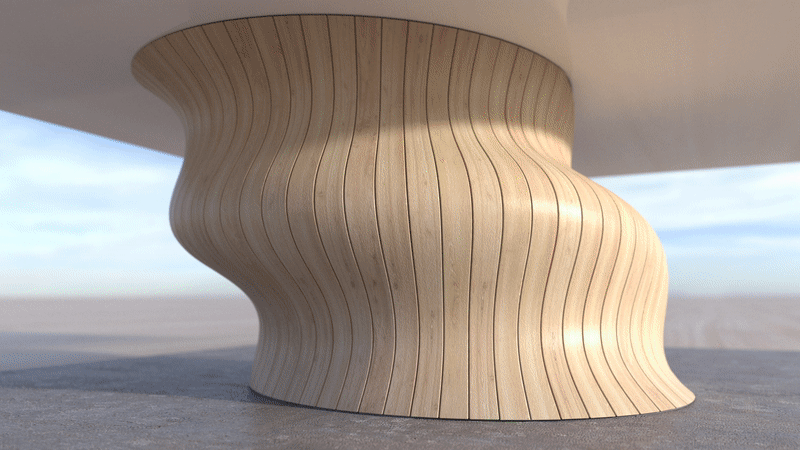
Fig.1: In this paper, we model a geodesic parallel mesh with a regular quad grid by choosing a geodesic direction and asking for the geodesic parallel angles constraint. We furthermore ask for equal edge lengths along parallel polylines to get a discrete surface isometric to a surface of revolution. Instead, with angle constraint, equal edge lengths along geodesic polylines, and the discrete Jacobi equation, we can model discrete developable surfaces.

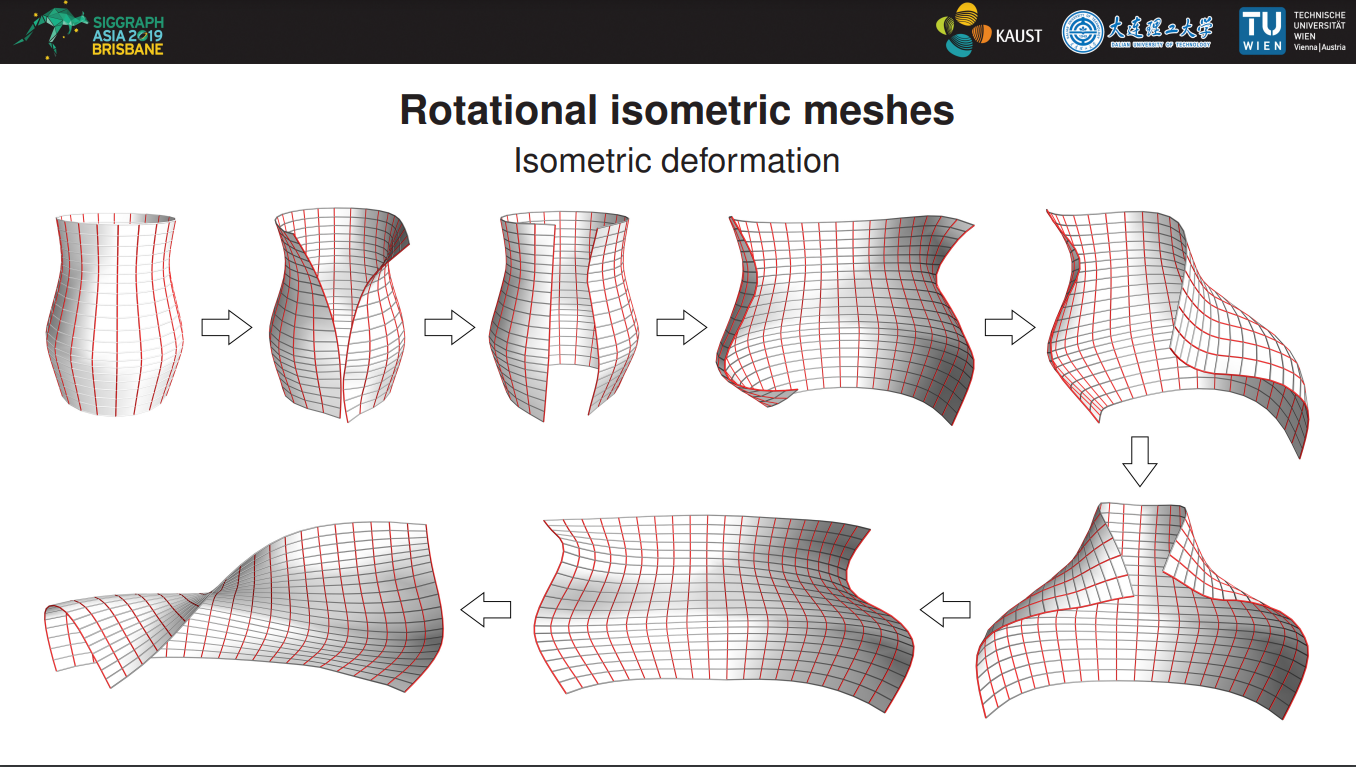
Fig.2: Cuting along a profile curve of the rotatioanl surface, isometrically deform it to get freeform patches.

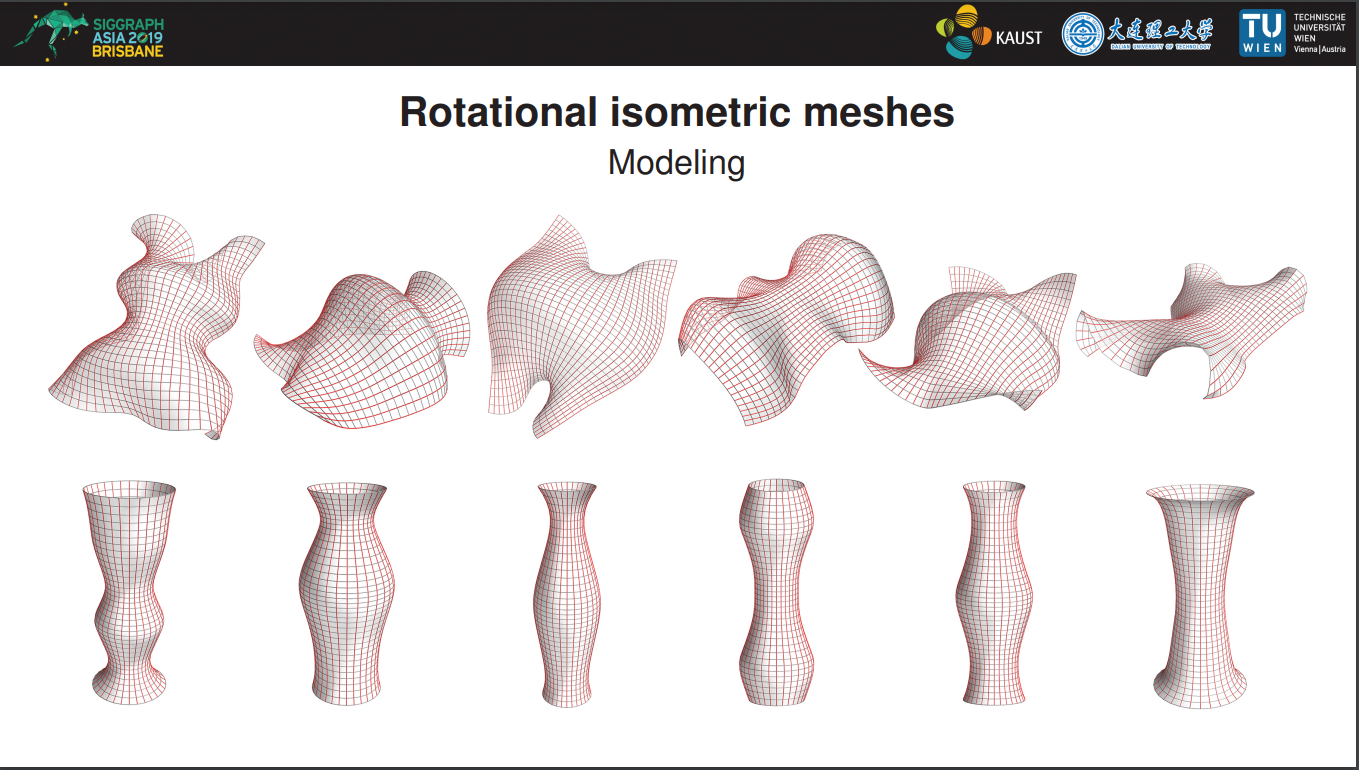
Fig.3: The variety of surface patches (top) isometric to surfaces of revolution (bottom).

Fig.4: Geodesic parallel meshes can approximate a nearly developable surface like for instance a folded felt. The process is the following. We first scanned a folded felt to get a mesh model. We start then from a planar quad mesh. With geodesic parallel and developability constraints on, we optimize for closeness with the scanned mesh. We observe a good approximation, and the corresponding surface of revolution is an almost right cylinder. On bottom right, the nearly developable surface has been developed into the plane. Also here we can observe small distortions.

Fig.5: Geodesic parallel meshes very naturally leads to real-world applications. First of all, geodesics on a surface can be easily materialized with thin elongated quadrilateral timber strips(straight strips). Moreover, parallel geodesics are fairly distributed over a surface. Geodesic parallel meshes are then well suited for the design of architectural geodesic gridshells. A design procedure can be the following. Given a freeform reference surface, we can cover the surface with a geodesic parallel mesh. In this way, we get a first family of geodesic curves on the surface. A second mesh with different orientation can be used for a second family of geodesic curves to get a network. If a reference surface is not given, a generic geodesic parallel mesh can be used as a reference for the second one. To test our design procedure, we built a small scale model made of straight wooden strips, shown on the left. Here we can see how well the model match our geodesic parallel mesh on the right.

GIF