Computer-Aided Design (CAD)

Caigui Jiang, Florian Rist, Hui Wang, Johannes Wallner, Helmut Pottmann

Small-scale cut and fold patterns imposed on sheet material enable its morphing into three-dimensional shapes. This manufacturing paradigm has been receiving much attention in recent years and poses challenges in both fabrication and computation. It is intimately connected with the interpretation of patterned sheets as mechanical metamaterials, typically of negative Poisson ratio. We here present an affirmative solution to a fundamental geometric question, namely the targeted programming of a shape morph. We use optimization to compute kirigami patterns that realize a morph between shapes, in particular between a flat sheet and a surface in space. The shapes involved can be arbitrary; in fact we are able to approximate any mapping between shapes whose principal distortions do not exceed certain bounds. This amounts to a solution of the so-called inverse problem for kirigami cut and fold patterns. The methods we employ include a differential–geometric interpretation of the morph, besides drawing on recent progress in geometric computing.

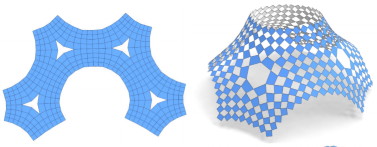
Fig.: Example of a quad-based metamaterial where a planar closed state morphs to a maximally open spatial state. The computation according to stages 1–3 involves a constant mean stretch mapping from a planar domain to the given design surface at right.

Fig.1: Auxetic behavior of regular squares can be considered by square corners gliding on the frame with same speed (the sizes of squares get scaled here).

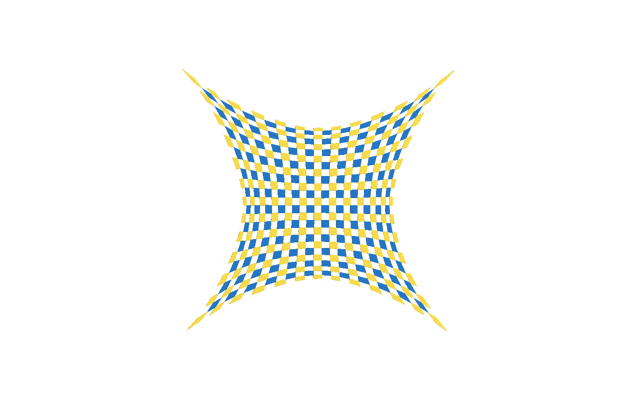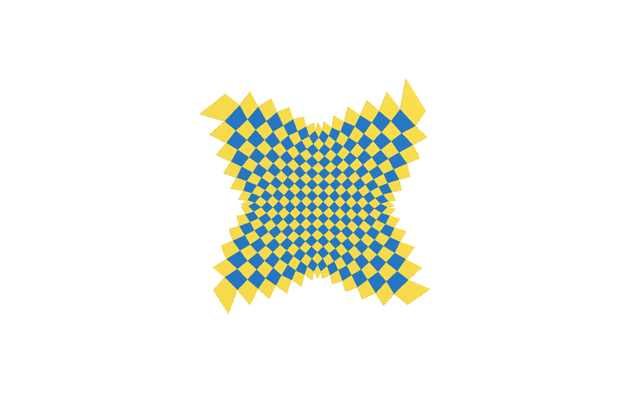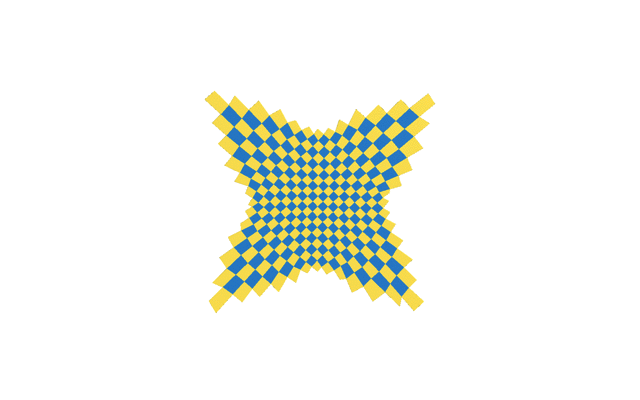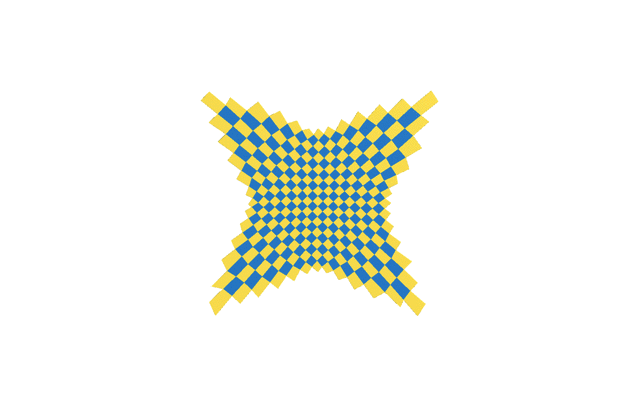
Fig.2: Joint optimization of quad-based metamaterials in closed state and fully open spatial state. “Fully open quads” means that all the hole quards are circular.

Fig.3: Lamps design from fully closed states to fully open states.

Fig.4: Roof design from fully closed planar states to fully open curved states.

Publication

Authors

PDF

Abstract

Figures

Video