Designing Asymptotic Geodesic Hybrid Gridshells

Publication

Computer-Aided Design (CAD)

Authors

Eike Schling∗, Hui Wang∗, Sebastian Hoyer, Helmut Pottmann (∗Joint first authors)

Abstract

Fabrication and assembly of freeform shells can be simplified significantly when controlling the curvature of structural elements during the design phase. This approach has produced fundamental insights to bending-active construction, using the elastic property of elements to form efficient load-bearing structures. This paper is focused on gridshells that are built from straight and flat slats. The slats are combined in two orientations, tangential and normal to the design surface, to create robust and versatile triangulated grids. For this purpose, we generate hybrid webs of asymptotic and geodesic paths on freeform surfaces. The research combines geometric computing with architectural building practice. We present a computational workflow for the design and interactive modification of hybrid asymptotic geodesic webs. At its core are discrete models that are based on concepts of differential geometry and allow to compute constrained structures within an optimization framework. The resulting webs are tested for architectural applications. We derive a strategy for the elastic erection process, in which geodesic lamellas are used as a guide and bracing of the spatial structure. Two architectural scenarios, a timber roof and a steel facade are presented. Their feasibility for construction is verified through prototypical joints and physical models. The research introduces a new class of networks and related surfaces and offers insights into the practical challenges of freeform construction from elastic slats.

Paper

paper

Slide

Figures

Fig.1: Numerical models of geodesic nets (1-2 row), Voss nets (3-4 row), asymptotic nets (5-6 row), AAG-webs (7-8 row), AGG-webs (9-10 row), AGAG-webs (11-12 row), their gridshells (second column) and corresponding developable strips’ unrollments (right columns).

Fig.2: Discussions in Fig.1 are confined to nets and webs of regular combinatorics, which limits the shape variety. For such meshes with a singularity of valence 6 or valence 8, we divide the web into 6 or 8 regular quad patches. Each patch is an AAG-web. Right column are two designs.

Applications

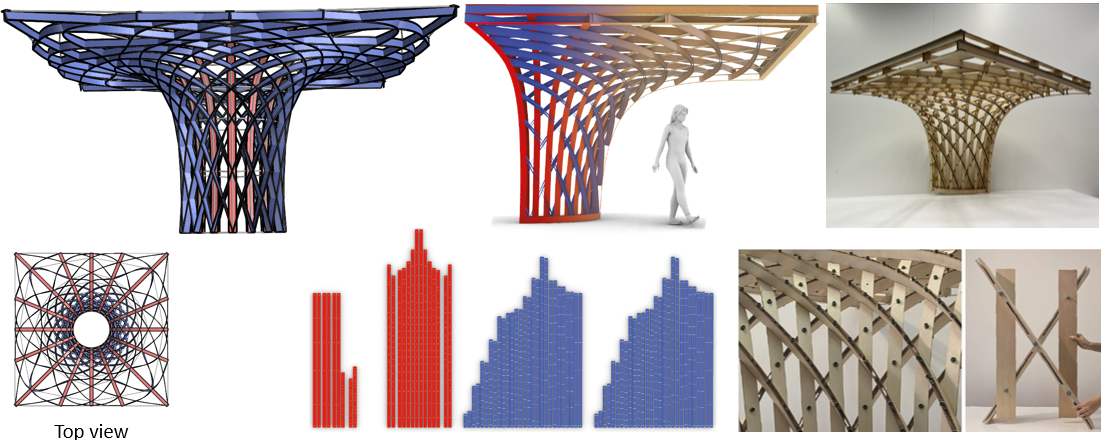
Fig.3: We designed and built a timber roof structure from straight lamellas. The Top and bottom mesh boundaries of the computed rotational AAG gridshell have square and circular shapes, respectively. The real model is one-quarter of it.

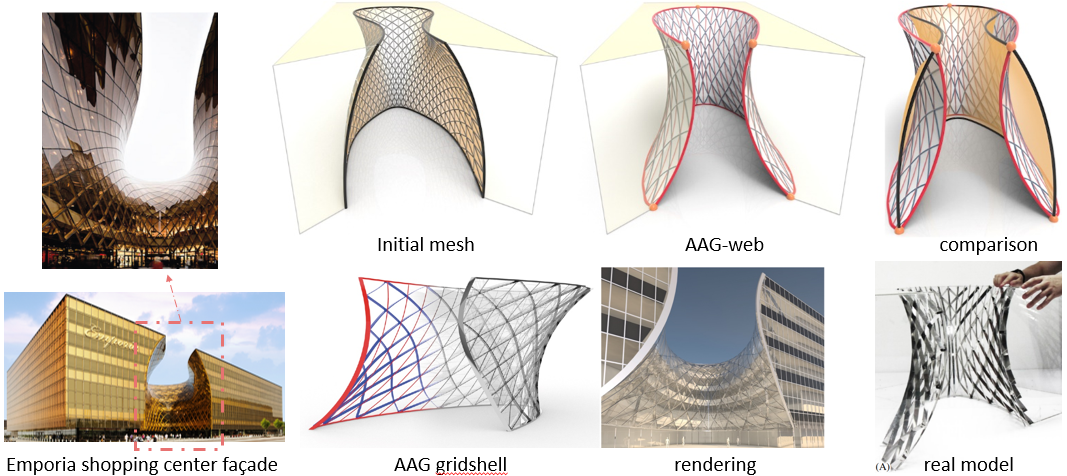
Fig.4: We redesigned the Emporia shopping center façade and successfully built a small-scaled steel AAG gridshell from straight rectangular steel slats. The original façade has obvious unsmooth supporting structures. Our optimized AAG-web approximates the shape with 4 original planar boundaries, the shell improves the structure’s appearance.

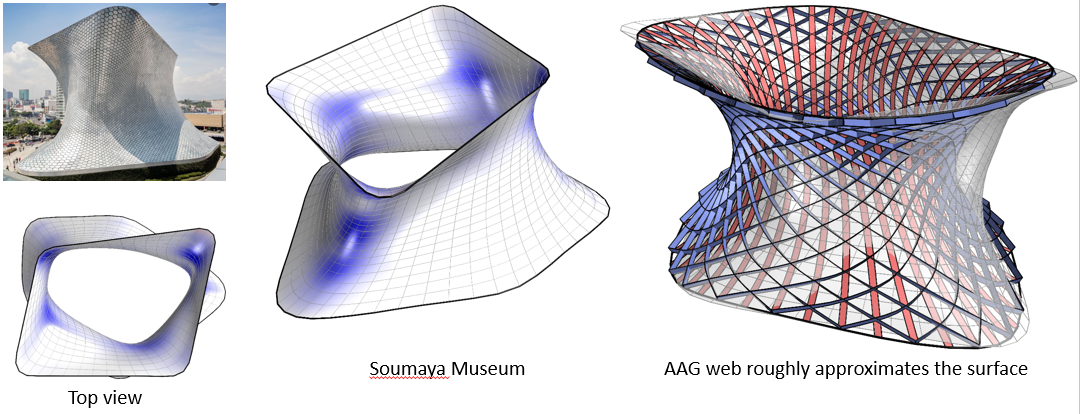
Fig.5: We roughly approximated the negatively curved part of the Soumaya Museum Model by an AAG web. This web results from the carefully-controlled optimization. Given any negatively curved mesh, we cannot directly approximate it to be an AGG or AAG-web. Only special shapes are possible. How to approximate a given curved shape is still an open question. A promising way to investigate the generation of webs is by using a level set approach. It will be our future work.

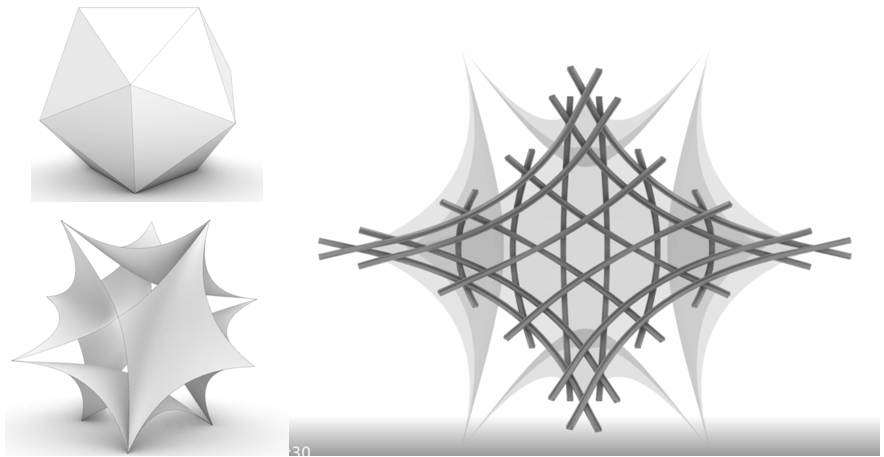
Fig.6: During the Winter Olympic Games Beijing 2022, many steel landscape sculptures called Xuerong Stars(namely Edelweiss Stars) appeared in front of the National Stadium and Ice Cube. They were designed by Prof. Weixin Huang’s team from Tsinghua University. These steel models are designed based on the regular icosahedron, where 6 pairs of triangular faces are used to form the congruent curved patches and the other 8 left triangular faces are deleted.

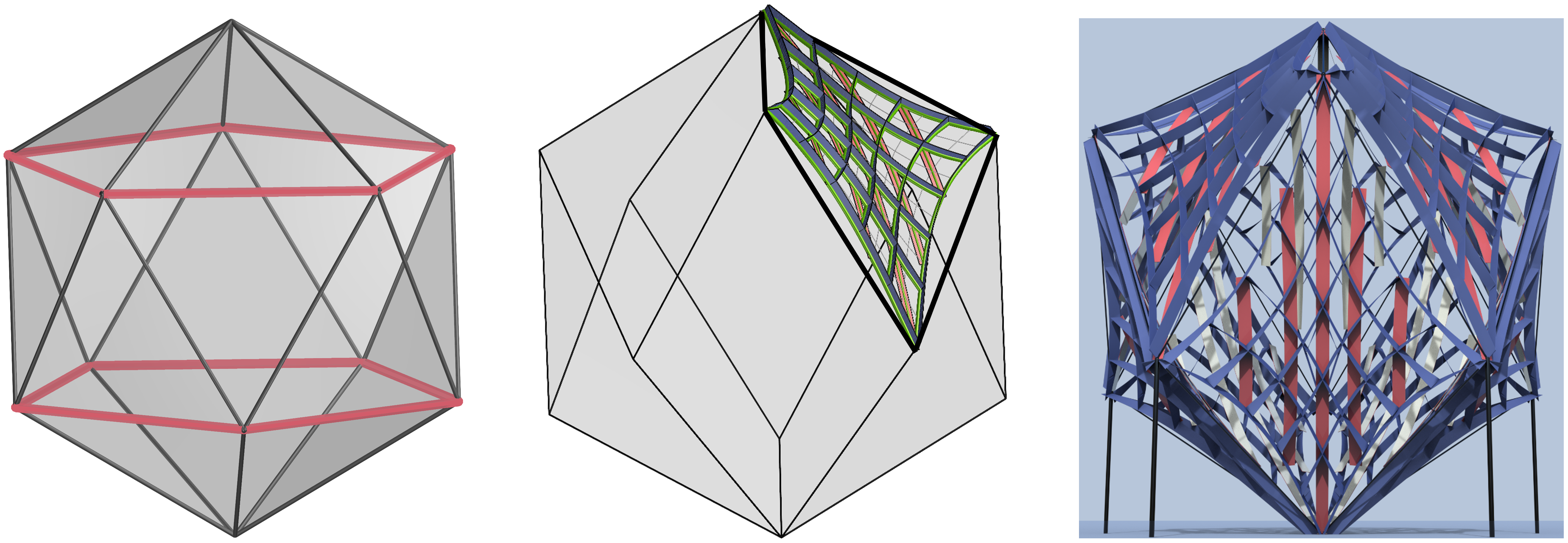
Fig.7: Still based on a regular icosahedron, I redesigned another AAG-gridshell with 20 patches congruent to each other. The red strips are tangent along the geodesic curves of each simple negatively-curved patch, and the other two families of diagonal strips are orthogonal along the asymptotic curves of the patch.

GIF

Video

Presentation video in YouTube and in Bilibili.

Open Source

Open source code has been released in Github :octocat:. Welcome!

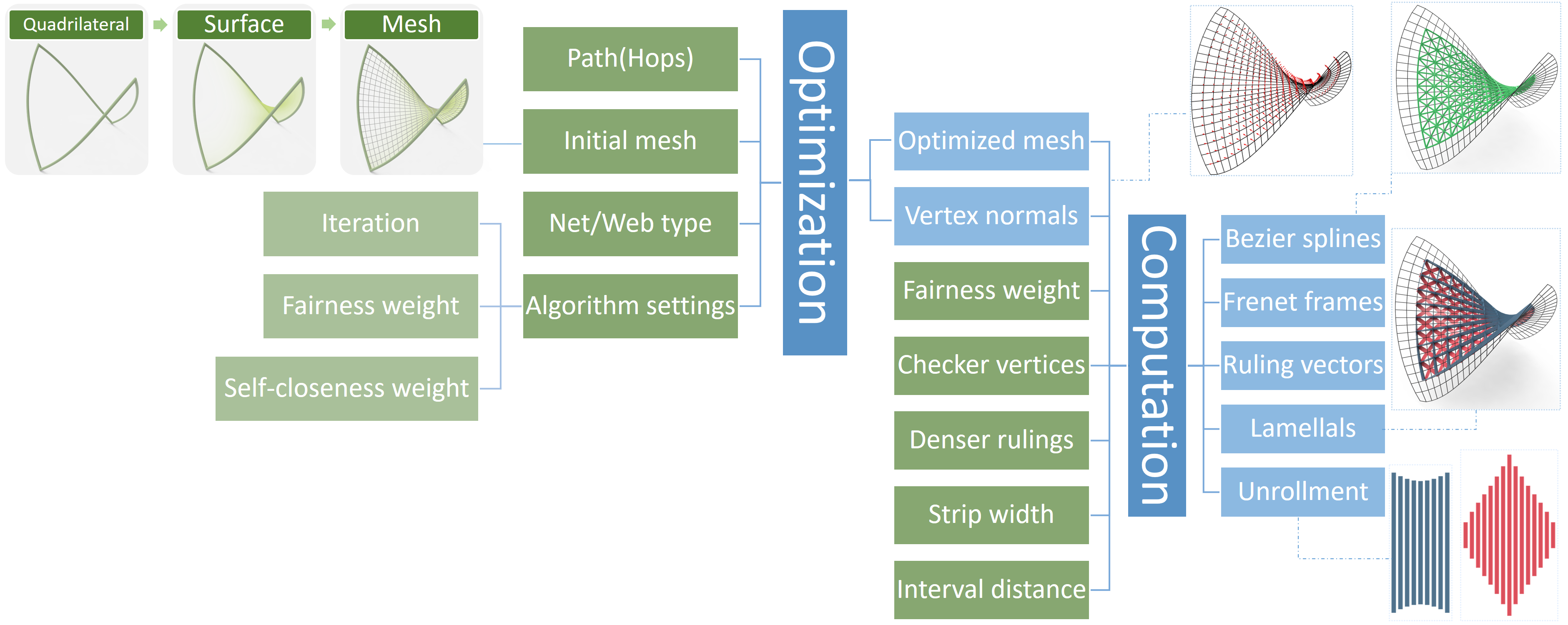
A user-friendly design tool has been realized by integrating the optimization into the CAD system Rhinoceros3D. Our plugin allows the user to define the main inputs to the optimization, the initial mesh, the web type, strip width and optimization parameters like the number of iterations and weights. The results, namely the optimized mesh, strip boundaries in piecewise quintic Bezier form, ruling vectors, the developable strips as well as their developments are returned as Rhinoceros3D geometry objects. The optimization is implemented in CPython and called from Grasshopper, Rhinoceros’ parametric design extension, using the Hops component. This allows the user to offload the actual computation to a more powerful remote machine, if desired. We will make our plugin available to the architectural community in the near future.